Complexitatea unui algoritm (timp și spațiu) în C++

De multe ori, pentru aceeași problemă, se găsesc metode diferite de rezolvare — mai exact, avem algoritmi diferiți. În funcție de cât de multe resurse se folosesc pentru rularea unui algoritm (în timp și în spațiu), se determină complexitatea algoritmului și mai apoi eficiența sa.

Ce reprezintă complexitatea unui algoritm?

Complexitatea unui algoritm reprezintă un mod de a măsura eficiența unui algoritm, în funcție de cât de multe resurse consumă acesta din punct de vedere al memoriei și al timpului.

Deși cu seturi mici de date eficiența unui algoritm este probabil neglijabilă, cunoașterea complexității unui algoritm este necesară în momentul în care ai o cantitate mai largă de date, iar metode mai ineficiente nu sunt folosibile.

Exemplu: complexitatea aflării numărului de divizori

Să luăm doi algoritmi diferiți care calculează numărul de divizori al unui număr n. Prima metodă ia toate numerele de la 1 la n și verifică pentru fiecare dacă este sau nu divizor al lui n, pe când a doua metodă ia doar numerele de la 1 la radicalul lui n, folosind o metodă mai eficientă (despre care poți citi în acest articol).

Prima metodă (ineficientă)

Codul arată astfel:

int nrdiv = 0;
for(int d = 1; d <= n; d++) {
    if(n % d == 0) {
        nrdiv++;
    }
}
cout << n << " are " << nrdiv << " divizori";

A doua metodă (eficientă)

Codul eficient arată astfel:

int nrdiv = 0;
for(int d = 1; d * d <= n; d++) {
    if(n % d == 0) {
        nrdiv++;
        if(d != n / d)
            nrdiv++;
    }
}
cout << n << " are " << nrdiv << " divizori";

Comparație

Se observă faptul că prima metodă merge de la 1 la n, astfel făcând n operații în total. Pe de altă parte, a doua metodă merge de la 1 până la radicalul lui n, astfel executând un maxim de sqrt(n) operații. Cum sqrt(n) ≤ n, al doilea algoritm va face, de regulă, mai puțini pași decât primul, astfel că îl considerăm mai eficient.

Acesta a fost un exemplu de complexitate a timpului, unde am numărat câți pași se efectuează în total pentru cei doi algoritmi. Similar se poate calcula și complexitatea de memorie, care vede cât de multă memorie se consumă.

Cum se calculează complexitatea unui algoritm

Complexitatea unui algoritm se calculează în funcție de câte operații se execută în program. Deoarece ne interesează strict complexitatea algoritmului, operațiile de citire și de afișare nu se iau de obicei în calcul — chiar dacă, pentru un vector, se citesc n numere, nu vom lua în considerare acest lucru.

Pentru restul operațiilor (precum comparații sau atribuiri), vom estima de câte ori apar acestea când se execută codul. Pentru exemplul de mai sus, prima metodă verifică pentru n numere (de la 1 la n), câte dintre ele sunt divizori. Astfel, vom estima că se execută n operații. Pentru a doua metodă, deoarece structura repetitivă parcurge numerele de la 1 la sqrt(n), atunci vom spune că acesta execută sqrt(n) operații.

De menționat este faptul că dacă se execută de mai multe ori n operații — de pildă, dacă avem două for-uri separate care merg de la 1 la n, deci în total 2 * n operații — atunci vom rotunji numărul total de operații la n.

Notația complexității cu Big O Notation

Complexitatea unui algoritm se notează cu O(…), unde … reprezintă numărul de operații calculat mai sus. Spre exemplu, pentru primul algoritm din exemplul de mai sus, spunem că are complexitatea O(n).

Notația cu O(…) — numită Big O Notation — se referă la cel mai defavorabil caz din algoritm. Spre exemplu, dacă am avea următoarea structură repetitivă care se oprește atunci când găsește un divizor:

for(int i = 2; i <= n; i++) {
    if(n % i == 0)
        break;
}

Chiar dacă există cazuri în care codul se oprește instant (n = 2, spre exemplu) sau foarte rapid (n = 3), vom lua cel mai rău caz posibil, atunci când n este un număr prim — astfel că vom nota complexitatea algoritmului cu O(n).

Diferența dintre complexitățile algoritmilor

În imaginea de mai jos se observă clar diferența complexităților în funcție de un anumit număr n:

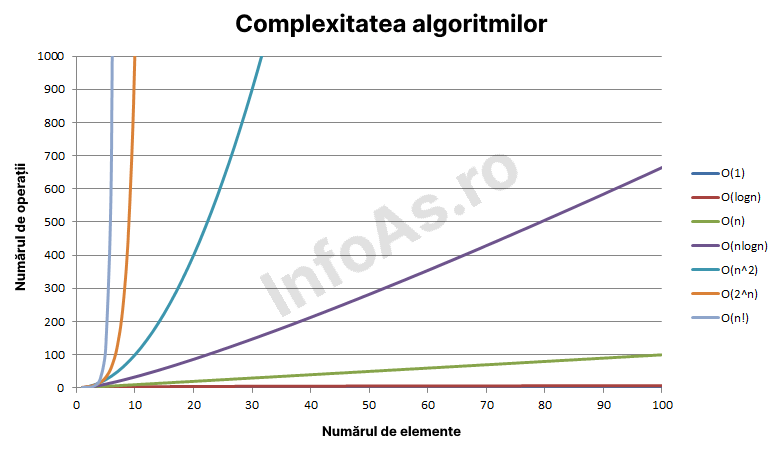
Vom lua fiecare tip de complexitate în parte și vom discuta despre aceasta.

Complexitatea constantă — O(1)

Complexitatea O(1) (constantă) reprezintă faptul că algoritmul execută instant (dintr-o singură operație) codul. Iată niște exemple de complexități constante:

• Adunarea a două numere: a + b;
• Aflarea sumei 1 + 2 + 3 + … + n: aceasta se află instant cu operația n * (n + 1) / 2;
• Aflarea parității unui număr, care se află instant cu operația n % 2.

Complexitatea logaritmică — O(log n)

Complexitatea logaritmică O(log n) sau O(log2 n) sugerează un algoritm prin care se întâmplă împărțiri repetate la 2 a numărului de elemente considerate. În acest sens, exemple relevante sunt:

• Căutarea binară: setul inițial (1, n) se împarte repetat la 2, ajungându-se în final la un singur element;
• Algoritmi Divide et Impera: această metodă de rezolvare este bazată pe principiul că se împarte problema în subprobleme de lungime jumătate;
• Căutare într-un arbore binar: de la fiecare nod mergem la fiul potrivit, astfel eliminând de fiecare date aproximativ jumătate din nodurile de verificat.

Complexitatea radical — O(sqrt n)

Complexitatea radical O(sqrt(n)) sau O(sqrt n) apare în algoritmi în care setul de date se împarte în mai multe seturi. În acest sens, avem ca exemplu:

• Operațiile cu divizorii unui număr: putem să prelucrăm divizorii unui număr parcurgând doar numerele de la 1 la sqrt(n).

Complexitatea liniară — O(n)

Pe departe cea mai întâlnită complexitate, complexitate liniară O(n) execută același număr de operații cu lungimea setului de date n. Exemple de complexități liniare se găsesc în algoritmii:

• Parcurgerea unui vector;
• Căutarea liniară în vector;
• Compararea a două șiruri de caractere.

Complexitatea O(n log n)

Complexitatea O(n log n) apare în cazul metodelor eficiente de sortare, precum:

• Merge Sort;
• Quick Sort;
• Heap Sort;

Complexitatea pătratică — O(n²)

Complexitatea pătratică O(n * n) sau O(n2) se folosește în cazul algoritmilor în care setul de date se parcurge de n ori. În acest sens, întâlnim următoarele exemple:

• Parcurgerea unei matrici pătratice cu latura n;
• Sortarea prin inserție: Insertion Sort;
• Sortarea prin selecție: Selection Sort;

Complexitatea algebraică sau polinomială — O(n^c)

Această complexitate se folosește în algoritmi ineficienți sau bruți. Complexități polinomiale pot fi O(n2), O(n3), ….

Complexitatea factorial — O(n!)

Complexități de tipul O(n!) apar în algoritmi ineficienți sau bruți. Iată câteva exemple:

• Calcularea tuturor permutărilor unui număr folosind metoda backtracking (fără afișare);
• Calcularea partițiilor unui număr folosind metoda backtracking (fără afișare);
• Alți algoritmi backtracking sau bruți.

Alte complexități

În algoritmi se pot îmbina complexitățile menționate mai sus, sau pot chiar să formeze complexități noi. Spre exemplu, algoritmul de generare a permutărilor are complexitatea O(n!), iar operația de afișare a elementelor unui vector are complexitatea O(n), astfel că un algoritm care calculează permutările unei submulțimi și afișează soluțiile are complexitatea O(n! * n).

Alte resurse sau bibliografie

• Imagine inițială cu complexitatea algoritmilor oferită de HackerEarth și tradusă în română
• mdcoroiu.ro: Complexitatea algoritmilor
• Wikipedia: Complexitate în timp
• UBBCluj: Analiza complexității — studiul eficienței algoritmilor
• Wikipedia: Big O notation